Две старушки: быстрая и медленная, «Софизмы, ребусы...». Сообщение #90 |

Здравствуйте, гость ( Вход | Регистрация )
Активные темы за последние суткиНовые сообщения с Вашего последнего посещенияГлавная страница форума |
Две старушки: быстрая и медленная, «Софизмы, ребусы...». Сообщение #90 |
 3.7.2016, 19:10 3.7.2016, 19:10
Сообщение
#1
|
|
 Бывший активный участник Группа: Пользователь Сообщений: 4440 Регистрация: 7.10.2014 Из: Королёв Пользователь №: 2324 |
Две старушки: быстрая и медленная Из пункта А в город Б отправилась в путь старушка «А». Одновременно из пункта Б в пункт А по той же дороге отправилась в путь старушка «Б» (быстрая). Ровно в полдень они встретились и, не останавливаясь, продолжили путешествие. Старушка «Б» пришла в пункт А в 4 часа дня, а старушка «A» пришла в пункт Б только в 9 часов вечера. Когда старушки отправились в путь? Если старушки вышли в путь одновременно, а пришли в пункты назначения в разное время, значит, они шли с разными скоростями. Изобразим эти скорости в виде векторов. 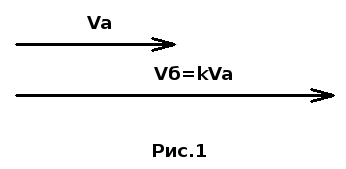 Va — скорость старушки «А», Vб — скорость старушки «Б». Решение задачи обеспечит то, что мы обозначили отношение этих скоростей буквой k. Старушки шли навстречу друг другу и в полдень встретились. 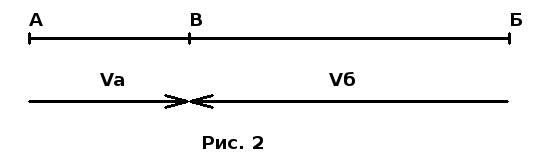 Поскольку в задаче мы имеем дело не с численными значениями скоростей, а только с их отношением, то векторы скоростей можем рисовать в любом масштабе, важно, чтобы одинаковом. Здесь их длины равны длинам соответствующих частей отрезка АБ, изображающего дорогу между пунктами А и Б. Поэтому на рисунке 2 длины векторов не только отображают скорости старушек, но и изображают пути, пройденные ими за время от выхода в путь до встречи. Всё, что можно сказать, глядя на рисунок 2, это: 1. Скорость старушки «А» в k раз меньше скорости старушки «Б»; 2. Скорость старушки «Б» в k раз больше скорости старушки «А»; 3. Путь, пройденный старушкой «А» до встречи, в k раз меньше пути, пройденного за это время старушкой «Б»; 4. Путь, пройденный старушкой «Б» до встречи, в k раз больше пути, пройденного за это время старушкой «А»; 5. После встречи старушке «А» предстоит пройти путь в k раз больший, чем она прошла; 6. После встречи старушке «Б» предстоит пройти путь в k раз меньший, чем она прошла. Здесь есть кое-что лишнее, но я хотел показать, как иногда полезно всесторонне охарактеризовать ситуацию, написав о ней всё, что можно. На следующем рисунке векторы нарисованы под теми участками дороги, которые старушки прошли после встречи. Масштаб векторов взят другой для того, чтобы длина вектора Vб была равна отрезку АВ. 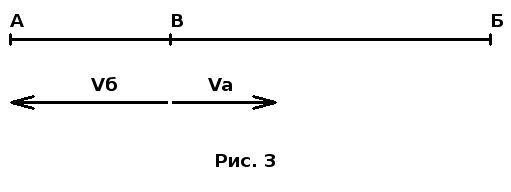 Об этих векторах можно сказать, что они не только отображают скорости старушек, но и изображают пути, пройденные ими за время от встречи до окончания путешествия старушкой «Б». Это время легко найти из условия задачи: после встречи старушка «Б» шла с 12 до 16 часов, то есть, 4 часа. Теперь всё внимание — старушке «А». Используем оставшуюся часть условия: старушка «А» после встречи шла с 12 до 21 часа, то есть, 9 часов. Отчего такая разница: 4 часа и 9 часов? Во-первых, после встречи старушка «А» должна была преодолеть расстояние ВБ, в k раз большее, чем старушка «Б», и если бы она прошла его со скоростью старушки «Б», то на остаток пути у неё ушло бы в k раз больше времени, чем у старушки «Б» на остаток её пути (АВ). Во-вторых, скорость у старушки «А» меньше в k раз, и это дополнительно увеличивает в k раз время преодоления остатка пути. Значит, k*k=9/4=2,25; отсюда находим k=1,5. Возвращаемся к рисунку 3. Путь ВБ старушка «А» прошла за 9 часов, а путь АВ в k=1,5 раза меньше пути ВБ. Значит, путь АВ (от выхода в путь до встречи) она прошла за время, в полтора раза меньшее, то есть, за 6 часов. Отматываем время от полудня назад на 6 часов и получаем ответ: старушки вышли в 6 часов утра. -------------------- Я такой же, как все: я не похож ни на кого другого.
|
|
|
|
 |
 24.9.2016, 22:28 24.9.2016, 22:28
Сообщение
#2
|
|
 Бывший активный участник Группа: Пользователь Сообщений: 4440 Регистрация: 7.10.2014 Из: Королёв Пользователь №: 2324 |
Другой метод решения этой задачи В школе, как помню, нас учили, что систему уравнений возможно решить, если количество уравнений равно количеству независимых переменных. Оказалось, что можно решить систему, если это условие не соблюдается. В этом случае среди независимых переменных есть такие, без которых нельзя составить уравнения, но по ходу решения они попадают под сокращение. Другие переменные встречаются в уравнениях, будто за круглыми столами, по двое, по трое, четверо и ведут не слышные нам переговоры о том, на какие окончательные числовые значения они в принципе согласны, если остальные возьмут на себя соответствующие обязательства. Иногда приходится приглашать «лишние» переменные, они помогют остальным договориться и потом уходят, говоря на прощание, что ни на что конкретное они не претендуют. Поэтому в совместном заявлении об итогах переговоров (когда объявляются численные значения всех переменных) о них не бывает ни слова. Покажем роль «лишних» переменных на примере решения этой задачи другим методом. Хотел написать, что это «графоаналитический метод», но Гугл по такому запросу выдал ссылки на недоступные моему пониманию тексты. Дополним текст задачи тем, что не высказано, но подразумевается: скорости каждой из старушек до и после встречи были одинаковы и постоянны. Решим задачу, воспользовавшись графиком движения. Это чертёж, каждая линия на котором отображает движение некоторого объекта, при этом каждая точка этой линии показывает, в какой точке пути находится (или находился, или планирует находиться) этот объект в выбранный момент времени. Шкала времени и шкала расстояний на графике движения являются равномерными (линейными), поэтому прямая линия на нём соответствует, независимо от направления наклона, движению с постоянной скоростью. Вертикальная линия соответствует неподвижному объекту, но это нам не пригодится. Начертим график движения, исходя из качественных характеристик путешествия старушек. 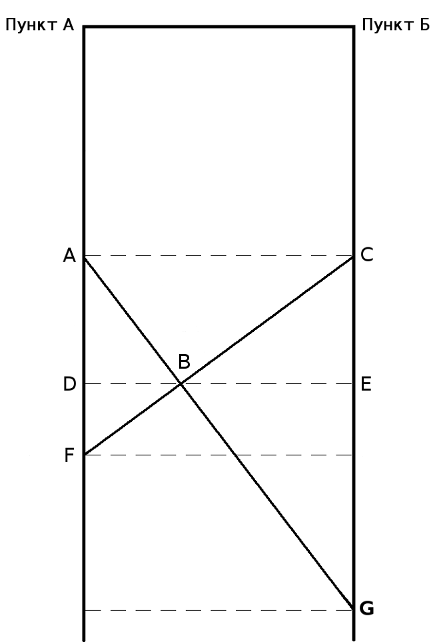 Рис. 4 Нахождению любого объекта в пункте А соответствует вертикальная линия с точкой А; нахождению в пункте Б — вертикальная линия с точкой С. Если на графике движения провести вспомогательую горизонтальную линию, соответствующую определённому моменту времени, то точки её пересечения с графиками движения объектов покажут положение этих объектов в этот момент. Расположению точек А и С на одной горизонтали соответствует одновременность начала путешествия обеими старушками. То, что точка G находится ниже точки F (насколько ниже — пока не уточняем), соответствует более позднему окончанию путешествия старушкой А. Пересечению графиков движения соответствует встреча объектов в пути. Так у нас появилась точка В — точка встречи старушек. Горизонтальная линия с точками В, D и Е соответствует времени встречи. Если начать чертить график движения с откладывания на оси времени моментов, известных из условия задачи и затем, произвольно задавая положение точки встречи, проводить через неё наклонные прямые, то после нескольких попыток можно решить задачу графически. Но точный ответ получим, если составим систему уравнений, основываясь на подобии треугольников, и решим её относительно величины AD (или CE). На рисунках 5 и 6 полдень отмечен как 12 часов, 4 часа дня — как 16 часов, а 9 часов вечера — как 21 час. 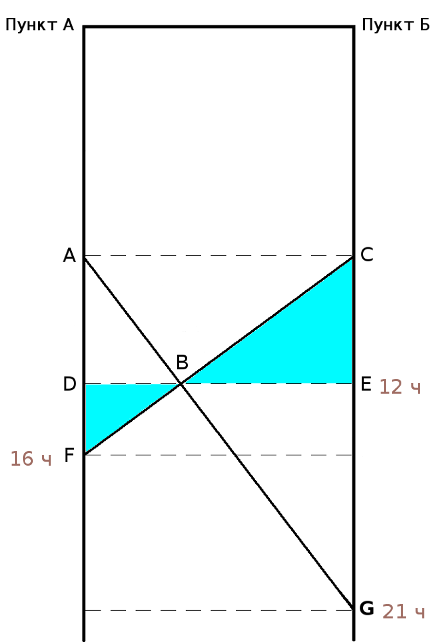 Рис. 5 Из подобия синих треугольников следует: 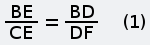 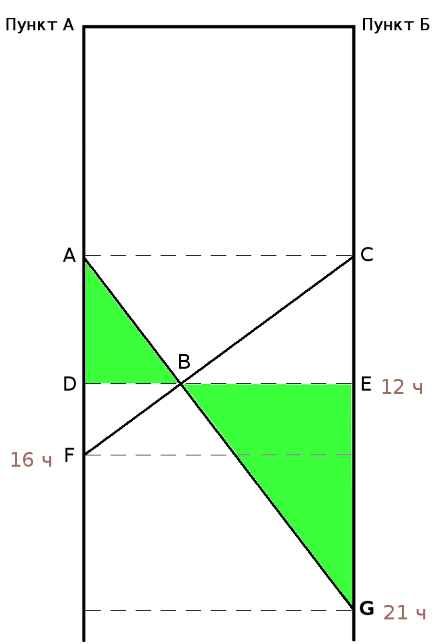 Рис. 6 Из подобия зелёных треугольников следует: 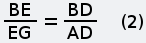 Последнее уравнение, которое нам подсказывает чертёж — AD=CE. Подставляем его в (1): 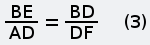 Уравнение (1) больше не нужно. Подставляем EG=9 в (2): 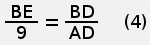 Уравнение (2) больше не нужно. Подставляем DF=4 в (3): 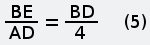 Уравнение (3) больше не нужно. Мы получили два уравнения (4) и (5) с тремя переменными BE, BD и AD. Нам ещё повезло: если бы мы составили уравнения на основании подобия треугольников CAF и BDF, ACG и BEG, то получили бы три уравнения с четырьмя переменными. Не убоявшись того правила, которое помним со школьных времён, продолжаем решать. Если взять (4), то чему равно BD? 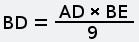 Если взять (5), то чему равно BD? 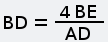 Из правых частей этих выражений составим равенство и дальше пояснения не требуются. 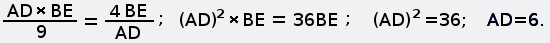 Старушки вышли в путь за 6 часов до полдня, то есть, в 6часов утра. Обе «лишние» независимые переменные — это горизонтальные отрезки, соответствующие расстояниям. Численные значения расстояний отсутствуют в условии задачи, поэтому они не могут появиться в ответе. Ещё можно рассуждать так: если чертёж растянуть по горизонтали до любой величины (как если бы он был начерчен на листе резины), то на уравнениях это никак не скажется, то есть, DB и ВЕ могут иметь любую величину, лишь бы отношение между ними не изменялось. Ввести их в рассмотрение заставила необходимость алгебраически отразить подобие треугольников. -------------------- Я такой же, как все: я не похож ни на кого другого.
|
|
|
|
  |

|
Текстовая версия | Сейчас: 23.4.2024, 16:35 |